ESTADISTICA: CONJUNTO POTENCIA O FAMILIAR

Conjuntos potencia

1.5.1. Un conjunto muy importante en la teoría de conjuntos es aquel que, dado un conjunto $x$ cualquiera, contiene todos los subconjuntos de este conjunto $x$ . Un conjunto así se llama conjunto potencia. Más exactamente, si $x$ es un conjunto, entonces el conjunto potencia de $x$ es el conjunto $\mathcal{P}(x)$ dado por

$\mathcal{P}(x)=\{y\mid y\subseteq x\}$ .

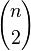1.5.2. Puesto que $\varnothing\subseteq\varnothing$ , $\mathcal{P}(\varnothing)=\{\varnothing\}$ , y por tanto $\mathcal{P}(\varnothing)$ contiene un solo elemento, y por ello $\mathcal{P}(\varnothing)\neq\varnothing$ . Sea $x$ un conjunto con $n$ elementos. Entonces, existen $n$ subconjuntos de $x$ con un solo elemento, $n\choose 2$ subconjuntos de $x$ con dos elementos, $n\choose 3$ subconjuntos de $x$ con 3 elementos, y así sucesivamente hasta llegar a los $n\choose n$ subconjuntos de $x$ con $n$ elementos. De este modo, $\mathcal{P}(x)$ tiene

$\sum_{i=0}^n {n\choose i}=(1+1)^n=2^n$

elementos, siendo esta última ecuación un caso particular del binomio de Newton. Como puede verse, el conjunto potencia $\mathcal{P}(x)$ de un conjunto $x$ contiene en general muchos más elementos que el conjunto $x$ , razón por la cual es difícil dar ejemplos de conjuntos potencia.

1.5.3. Nótese que $a\in x$ equivale a $\{a\}\in\mathcal{P}(x)$ .

1.5.4. Algo más interesante y conveniente de notar es que

$\bigcup_{x\in\mathcal{P}(X)}x=X$

para cualquier conjunto $X$ . En efecto, pues de $a\in\bigcup_{x\in\mathcal(X)}x$ , se sigue $a\in x$ para algún $x\in\mathcal{P}(X)$ , es decir, para algún $x\subseteq X$ , por lo que $a\in X$ . Recíprocamente, si $a\in X$ , entonces $a\in x$ para algún conjunto $x\in\mathcal{P}(X)$ (e.g. el conjunto $\{a\}\subseteq X$ ), luego $a\in\bigcup_{x\in\mathcal{P}(X)}x$ .

1.5.5. Como hecho más general, si $C$ es una colección de subconjuntos de un conjunto $X$ , es decir si $C\subseteq\mathcal{P}(X)$ , entonces $\bigcup_{x\in C}x\subseteq X$ .

1.5.6. Ahora vamos a generalizar algunas leyes a cerca de la unión e intersección de conjuntos. Primero, considérese un conjunto dado $u$ , y luego considérese una colección $C$ de subconjuntos de $u$ . Fórmese la unión

$\bigcup_{x\in C}x$ ,

un subconjunto de $u$ . El complemento

$\mathcal{C}\left(\bigcup_{x\in C}x\right)$ ,

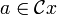es un subconjunto de $u$ . Si $a\in\mathcal{C}(\bigcup_{x\in C}x)$ , entonces $a\notin\bigcup_{x\in C}x$ , por lo que $a\notin x$ para todo $x\in C$ , y puesto que $x\subseteq u$ , el complemento $\mathcal{C}x$ existe y $a\in\mathcal{C}x$ para todo $x\in C$ . Así, $a\in\bigcap_{x\in C}\mathcal{C}x$ . El conjunto anterior es en efecto una intersección de los conjuntos de una colección, a saber

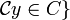$C'=\{y\mid y\subseteq v$ y $\mathcal{C}y\in C\}$ .

Sea $u$ un conjunto y $C$ una colección de subconjuntos de $u$ . El resultado anterior, y otro cuya demostración se deja como un sencillo ejercicio al lector, se presentan a continuación:

$\mathcal{C}\left(\bigcup_{x\in C}x\right)=\bigcap_{x\in C}\mathcal{C}x$

$\mathcal{C}\left(\bigcap_{x\in C}x\right)=\bigcup_{x\in C}\mathcal{C}x$

Las proposiciones anteriores son una generalización de las leyes de De Morgan.

COMENTARIO: Se dice que es el conjunto de todos los subconjuntos.

ESTADISTICA

sábado, 20 de septiembre de 2008

CONJUNTO POTENCIA O FAMILIAR

Conjuntos potencia

No hay comentarios:

Datos personales

Archivo del blog