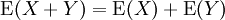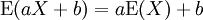lunes, 6 de octubre de 2008
EL AULA VIRTUAL
LA IMPORTANCIA DEL BLOG
lunes, 29 de septiembre de 2008
http://www.youtube.com/watch?v=wPmi1pcoDq8
jueves, 25 de septiembre de 2008
ESPERANZA MATEMATICA
Esperanza matemática
En estadística la esperanza matemática (o simplemente esperanza) o valor esperado de una variable aleatoria es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso. Por ejemplo, en un juego de azar el valor esperado es el beneficio medio.
Si todos los sucesos son de igual probabilidad la esperanza es la media aritmética.
Definición
Para una variable aleatoria discreta con valores posibles  y sus probabilidades representadas por la función de masa p(xi) la esperanza se calcula como:
y sus probabilidades representadas por la función de masa p(xi) la esperanza se calcula como:
Para una variable aleatoria continua la esperanza se calcula mediante la integral de todos los valores y la función de densidad 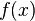 :
:
![E[X]=\int_{-\infty}^\infty x f(x)dx \,\!](http://upload.wikimedia.org/math/0/1/e/01ee197ad5dbb61b90d3ed7de412f720.png)
- o
![\operatorname{E}[X] = \int_\Omega X\, \operatorname{d}P \,\!](http://upload.wikimedia.org/math/2/b/b/2bb82da2aad67daf5519781e29dc4016.png)
La esperanza también se suele simbolizar con ![\mu = E[X] \,\!](http://upload.wikimedia.org/math/3/2/7/3279ba1ddb2ac80fce25a62bee4a55f4.png)
Las esperanzas ![E[X^k] \,\!](http://upload.wikimedia.org/math/f/7/1/f71df20458573663d1d38537e4e2b082.png) para
para  se llaman momentos de orden
se llaman momentos de orden  . Más importantes son los momentos centrados
. Más importantes son los momentos centrados ![E[(X-E[X])^k] \,\!](http://upload.wikimedia.org/math/a/1/2/a1293ec70351b19f815480e7e2c63840.png) .
.
No todas las variables aleatorias tienen un valor esperado. Por ejemplo, la distribución de Cauchy no lo tiene.
Propiedades
La esperanza es un operador lineal, ya que:
Combinando estas propiedades, podemos ver que -
donde  e
e 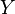 son variables aleatorias y
son variables aleatorias y  y
y 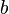 dos constantes cualesquiera.
dos constantes cualesquiera.
COMENTARIO: tiene por objeto calcular el promedio de los resultados ponderados por la probabilidad de que sucedan cada uno de los resultados posibles.
ARBOL DE PROBABILIDAD
miércoles, 24 de septiembre de 2008
LOS EVENTOS PUEDEN SER
INDEPENDIENTES: Estos no se ven afectados por otros.
DEPENDIENTES: cuando un evento afecta la probabilidad de ocurrencia de otra.
NO EXCLUYENTRES ENTRE SI: es cuando la ocurrencia de uno de elloss no impide que ocurra el otro.
AXIOMAS
Axiomas de probabilidad
Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función que definimos sobre unos sucesos determine consistentemente valores de probabilidad sobre dichos sucesos.
La probabilidad P de un suceso E, denotada por P(E), se define con respecto a un "universo" o espacio muestral Ω, conjunto de todos los posibles sucesos elementales, tal que P verifique los Axiomas de Kolmogórov, enunciados por el matemático ruso de este nombre en 1933. En este sentido, el suceso E es, en términos matemáticos, un subconjunto de Ω.
Axiomas de Kolmogórov
Dado un conjunto de sucesos elementales, Ω, sobre el que se ha definida una σ-álgebra (léase sigma-algebra) σ de subconjuntos de Ω y una función P que asigna valores reales a los miembros de σ, a los que denominamos "sucesos", diremos que P es una probabilidad sobre (Ω,σ) si se cumplen los siguientes tres axiomas.
Primer axioma
La probabilidad de un suceso A es un número real mayor o igual que 0.
La probabilidad de un suceso es un número positivo o nulo.
Segundo axioma
a 1.
Ω representa todas las posibles alternativas y se denomina suceso seguro.
Tercer axioma
entonces:
 .
.
Según este axioma se puede calcular la probabilidad de un suceso compuesto de varias alternativas mutuamente excluyentes sumando las probabilidades de sus componentes.
Propiedades que se deducen de los axiomas
De los axiomas anteriores se deducen otras propiedades de la probabilidad:
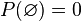 donde el conjunto vacío
donde el conjunto vacío  representa en probabilidad el suceso imposible
representa en probabilidad el suceso imposible- Para cualquier suceso
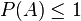

- Si
 entonces
entonces 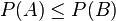

En términos más formales, una probabilidad es una medida sobre una σ-álgebra de subconjuntos del espacio muestral, siendo los subconjuntos miembros de la σ-algebra los sucesos y definida de tal manera que la medida del total sea 1. Tal medida, gracias a su definición matemática, verifica igualmente los tres axiomas de Kolmogórov. A la terna formada por el espacio muestral, la σ-álgebra y la función de probabilidad se la denomina Espacio probabilístico, esto es, un "espacio de sucesos" (el espacio muestral) en el que se han definido los posibles sucesos a considerar (la σ-álgebra) y la probabilidad de cada suceso (la función de probabilidad).
Como ejemplo se puede tomar como espacio muestral a los posibles resultados al arrojar un dado corriente  , tomaremos como σ-algebra todos los subconjuntos posibles de Ω (que en matemáticas se denota por
, tomaremos como σ-algebra todos los subconjuntos posibles de Ω (que en matemáticas se denota por  ) y como función de probabilidad
) y como función de probabilidad

Es fácil comprobar que esta función verifica los tres axiomas de Kolmogórov y, por tanto, consituye una probabilidad sobre este conjunto.
 , puesto que es el cociente de dos números positivos
, puesto que es el cociente de dos números positivos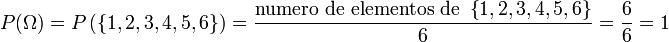
- Si
 de tal manera que
de tal manera que  entonces
entonces
-
- con lo que
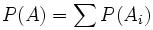
- con lo que
![E[X]=\sum_{i=1}^{n} x_i p(x_i) \,\!](http://upload.wikimedia.org/math/a/3/1/a314743e00cbe03ed42a3b5c93aeea12.png)