Intersección de conjuntos
En la teoría de conjuntos, la intersección es una operación binaria en el conjunto de todos los subconjuntos de un U, Conjunto universal, dado. Por la cual a cada par de conjuntos A y B de U se le asocia otro conjunto: 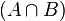 de U.
de U.
Si A y B son dos de ellos entonces su intersección se simboliza y se define como:
La intersección de A y B, es el conjunto de elementos x de U, tal que, x pertenezca a A, y que, x pertenezca a B.
Esta operación es conmutativa, asociativa, tiene neutro y tiene inverso:
donde:
 es el complemento de A.
es el complemento de A.
Por lo tanto el conjunto potencia de nuestro universo U y la operación  forman una estructura algebraica tipo grupo abeliano.
forman una estructura algebraica tipo grupo abeliano.
COMENTARIO: la interseccion es cuando se forma un conjunto que contine los elementos de A que al mismo tiempo estan en B.


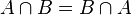




No hay comentarios:
Publicar un comentario