viernes, 29 de agosto de 2008

DIFERENCIA

Diferencia de conjuntos

Diferencia de conjuntos: A-B

Diferencia de conjuntos: B-A

Sean A y B dos conjuntos cualesquiera. En teoría de conjuntos, se denomina conjunto diferencia de A y B, y se representa por A -B o por A \ B, al conjunto formado por todos los elementos que están en A, pero no están en B.

Definición formal

Sean A y B dos conjuntos. La diferencia de conjuntos A - B es

$A - B = \{ x \in A \; \land \; x \not\in B \}$

Los elementos que pertenecen a la diferencia de conjuntos $A - B$ son aquellos elementos que pertenecen a A y no pertenecen a B.

Ejemplos

Si A = {a, b, c, d} y B = {b, d}; la diferencia de conjuntos A - B es

A - B = {a, c}.

Si A = { a, b, c, d } y B = { c, d, e, f }; entonces A - B = { a, b }

Si W = {x / x impar y x < z =" {">

W - Z = {1,3,5}

Z - W = {8,10,12,13}

Observaciones

La notación más utilizada es A - B, si bien algunos autores también utilizan la notación A \ B.
La diferencia de conjuntos no es conmutativa.
Los elementos de la intersección no se consideran parte de la Diferencia de Conjuntos.

Si A y B son conjuntos disjuntos, entonces la diferencia de conjuntos es:

$A - B = A \,$

$B - A = B \,$

COMENTARIO : es cuando los elementos de un conjunto que no se encuentren en el otro conjunto forman otro conjunto.

martes, 26 de agosto de 2008

INTERSECCION

Intersección de conjuntos

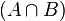En la teoría de conjuntos, la intersección es una operación binaria en el conjunto de todos los subconjuntos de un U, Conjunto universal, dado. Por la cual a cada par de conjuntos A y B de U se le asocia otro conjunto: $(A\cap B)$ de U.

Si A y B son dos de ellos entonces su intersección se simboliza y se define como:

$A\cap B= \{ x\in U \mid \ x \in A \ \land \ x \in B \}$

La intersección de A y B, es el conjunto de elementos x de U, tal que, x pertenezca a A, y que, x pertenezca a B.

Esta operación es conmutativa, asociativa, tiene neutro y tiene inverso:

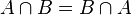
$A\cap B=B\cap A$

$(A\cap B)\cap C=A\cap (B\cap C)$

$A\cap\varnothing=\varnothing\cap A=\varnothing$

$A\cap A^c=A^c\cap A=\varnothing$

donde:

$A^c=\{x\in U\mid x\notin A\}$ es el complemento de A.

Por lo tanto el conjunto potencia de nuestro universo U y la operación $\cap$ forman una estructura algebraica tipo grupo abeliano.

COMENTARIO: la interseccion es cuando se forma un conjunto que contine los elementos de A que al mismo tiempo estan en B.

DIAGRAMA DE VENN

Diagrama de Venn

Los diagramas de Venn son ilustraciones usadas en la rama de la matemática conocida como teoría de conjuntos. Estos diagramas se usan para mostrar gráficamente la relación matemática o lógica entre diferentes grupos de cosas (conjuntos), representando cada conjunto mediante un óvalo o círculo. La forma en que esos círculos se sobreponen entre sí muestra todas las posibles relaciones lógicas entre los conjuntos que representan. Por ejemplo, cuando los círculos se superponen, indican la existencia de subconjuntos con algunas características comunes.

COMENTARIO: se dice que este diagrama se usa para mostrar graficamente la relacion logica que hay entre diferentes conjuntos.

UNION DE CONJUNTOS

Unión de conjuntos

En la teoría de conjuntos, la unión de conjuntos es una operación binaria en el conjunto de todos los subconjuntos de un U, Conjunto universal, dado. Por la cual a cada par de conjuntos A y B de U se le asocia otro conjunto: $(A\cup B)$ de U.

Si A y B son dos conjuntos, entonces su unión es:

$A \cup B= \{ x \in U \mid \ x \in A \ \vee \ x \in B \}$

La unión de A y B, es el conjunto de elementos x de U, tal que, x pertenezca a A, o que, x a pertenezca a B.

Esta operación es conmutativa, asociativa y tiene Elemento neutro.

$A \cup B = B \cup A$

$(A \cup B) \cup C = A \cup (B \cup C)$

$A \cup \varnothing = \varnothing \cup A = A$

$A \cup A^c = A^c \cup A = U$

COMENTARIO: se dice que es una operacion binaria en el conjunto de todos los subconjuntos de un conjunto universal.

TEORIA DE CONJUNTOS

teoría de conjuntos

Diagrama de Venn que muestra un conjunto

A

contenido en otro conjunto

U

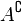
y su diferencia $A^\complement$

La teoría de conjuntos es una división de las matemáticas que estudia los conjuntos. El primer estudio formal sobre el tema fue realizado por el matemático alemán Georg Cantor en el Siglo XIX y más tarde reformulada por Zermelo.

El concepto de conjunto es intuitivo y se podría definir como una "colección de objetos"; así, se puede hablar de un conjunto de personas, ciudades, lapiceros o del conjunto de objetos que hay en un momento dado encima de una mesa. Un conjunto está bien definido si se sabe si un determinado elemento pertenece o no al conjunto. El conjunto de los bolígrafos azules está bien definido, porque a la vista de un bolígrafo se puede saber si es azul o no. El conjunto de las personas altas no está bien definido, porque a la vista de una persona, no siempre se podrá decir si es alta o no, o puede haber distintas personas, que opinen si esa persona es alta o no lo es. En el siglo XIX, según Frege, los elementos de un conjunto se definían sólo por tal o cual propiedad. Actualmente la teoría de conjuntos está bien definida por el sistema ZFC. Sin embargo, sigue siendo célebre la definición que publicó Cantor

comentario:

en si la teoria de conjuntos es una divicion de las matematicas que estudia los conjuntos desde sus distintos subtemas como lo son la union, interseccion etc... de conjuntos

Igualdad entre conjuntos. Subconjuntos y Superconjuntos

Igualdad de conjuntos

Dos conjuntos $~A$ y $~B$ se dicen iguales, lo que se escribe $~A = B$ si constan de los mismos elementos. Es decir, si y solo si todo elemento de $A$ está también contenido en $B$ y todo elemento de $B$ está contenido en $A$ . En símbolos:

comentario:
esto se da cuando dos conjuntos tienen elementos iguales...

ESTADISTICA